Prev Section 13.2: Développement des technologies
Up Chapitre 13: Dynamique des industries et des marchés
Section 13.4: Application : Nelson & Winter simplifié Next
13.3 Un modèle simple de dynamique industrielle basé sur les routines
Dans la lignée des premiers modèles développés par Nelson et Winter, la quasi-totalité des modèles évolutionnistes de la dynamique industrielle utilisent les routines pour représenter la rationalité procédurale des firmes.
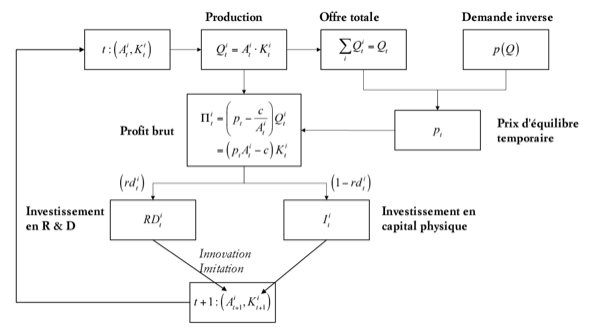
Le modèle initiale de [Nelson, 1982] possède la vertu d’être extrêmement simple et on peut le présenter sous la forme d’un diagramme (voir Figure 13.2↓) [F] [F] Pour une présentation plus détaillée de ce modèle consulter https://yildizoglu.fr/nelwin/ où il est aussi possible de faire des simulations en ligne pour étudier le comportement de ce modèle. Ce modèle a aussi été présenté dans [Nelson, 1982].. Dans ce modèle les technologies sont à rendements constants et le progrès technique n’est pas incorporé au stock de capital (sous la forme de générations successives de machines par exemple). Grâce à son investissement en R&D, chaque firme a la possibilité de profiter de progrès technique et d’augmenter la productivité
de son capital physique
.
L’équation du profit brut dans la Figure 13.2↑ montre clairement que l’augmentation de la productivité influence positivement la marge unitaire de la firme. Etant donné le coût d’utilisation du capital,
, dans une industrie où le prix baisse continûment du fait d’une expansion de l’offre globale, la seule possibilité de survie pour une firme est d’augmenter sa productivité, de manière à réduire son coût moyen de production
.
Dans la version originale de ce modèle les firmes utilisent des règles de comportement très simples pour l’investissement en R&D :
. Il n’existe alors aucun apprentissage au niveau des firmes. Le seul apprentissage peut avoir au niveau de la population : si le comportement d’innovation des firmes est initialement diversifié, celles qui utilisent une règle plus performante vont voir leurs parts de marché augmenter au détriment des autres firmes.
Ce modèle contient donc trois principaux blocs :
- Comportements sur le marché : offres, demande, prix de marché, profits;
- Changement technique : innovation et imitation (stochastiques), productivités;
- Dynamique du capital : investissement, dépréciation et stock de capital.
13.3.1 Comportements sur le marché
L’offre individuelle résulte directement du stock de capital accumulé avec une technologie est linéaire :
est la productivité du capital (
: le coefficient de capital) de la firme
à la période
et
représente le stock de capital de la firme.
L’ offre totale découle simplement de l’agrégation des offres individuelles :
s’il y a
firmes sur le marché.
La fonction de demande utilisée par Nelson & Winter est à élasticité constante et l’équilibre intra-période détermine le prix de marché :
Pour simplifier, les auteurs de modélise pas les interactions sur le marché du produit, en résumant la situation sur ce marché par un équilibre de court terme.
Le profit brut est donné par
de sorte que dans un marché où le prix baisse, la seule possibilité de survie pour la firme est le progrès technique qui diminuerait le coût moyen
.
Le taux de profit net sur le capital peut être calculé en intégrant les coûts de la R&D :
Le profit net de la firme peut alors s’écrire de la manière suivante :
13.3.2 Progrès technique
La productivité des firmes est modifiée à chaque période par le biais de leur innovations et imitations des concurrents.
Innovations
Etant donnée la nature non-monotone et stochastique de la relation entre les efforts de recherche des firmes (leurs investissements en R&D) et le résultats de ces efforts (leurs innovations) constatée dans la littérature empirique, l’innovation est modélisée comme un processus stochastique en deux étapes :
- Un tirage binomiale détermine si la firme a eu la chance de découvrir une innovation (évènement
- Si oui, on fait un second tirage détermine le résultat de l’innovation où représente le niveau de connaissance individuelle de la firme , tandis que qui est la productivité moyenne de l’industrie représente le niveau de connaissance globale de l’industrie. Le temps peut représenter à son tour la présence d’une dynamique des connaissances indépendantes e celles développées au sein de cette industrie.
Nelson & Winter considère trois régimes technologiques très simplifiés dans ce modèle minimaliste :
- Progrès technique tiré par la science : où représente l’évolution latente de la productivité qui provient de l’activité de recherche réalisée en dehors de l’industrie en question (par exemple au sein des universités). Cette spécification correspond à une situation où l’innovation est surtout basée sur la science (car indépendantes de l’activité des firmes).
- Innovations cumulatives au niveau des firmes car la firme n’a besoin que de ses connaissances individuelles pour innover de sorte qu’une firme qui prend de l’avance sur ses concurrents pourra profiter de cette avance pour avancer encore plus rapidement et dominer son secteur.
- Innovations incrémentales ou systémiques correspondant à des secteur de produits-système dans lesquels chaque firme a besoin du stock de connaissances collectif de son industrie pour avancer (le niveau des connaissances de l’industrie étant représenté ici par la productivité moyenne). Dans un tel régime, il est très difficile pour une firme de faire cavalier seul (contrairement au régime précédent, par exemple), car en innovant, elle ouvre aussi le champs des possibles pour les autres firmes.
Imitations et diffusion des technologies
Une autre source d’apprentissage pour la firme vient de la possibilité d’imiter la technologie de ses concurrents, en dédiant un effort particulier à ce but. Comme Nelson & Winter désirent comparer la performance des firmes qui cherchent à devenir les leaders de l’industrie avec celle des firmes qui se contenteraient d’être des suiveurs, ils distinguent la R&D innovatrice de la R&D d’imitation (cela permet notamment de vérifier les conditions d’émergence des faits stylisés de type la malédiction du gagnant (on a souvent observé qu’une firme qui développe la première une technologie ou un produit finit par être épuisée par l’effort d’un tel développement et se trouve détrôné par un concurrent qui bénéficie de l’expérience de la première – winner’s curse), ou ou dela possibilité pour des firmes suiveurs de bénéficier d’une performance satisfaisante en économisant les coûts de la R&D d’innovation.
La réussite de l’imitation (l’évènement
) par la firme i est déterminée par un seul tirage binomiale :
Si l’imitation est réussie alors la firme obtient (de manière quelque peu miraculeuse!) la meilleure technologie de l’industrie sans aucun coût supplémentaire :
où
est la productivité maximale actuelle dans l’industrie.
Finalement, la productivité dont va bénéficier le capital de la firme pendant la période suivante est donnée par la meilleure des trois sources potentielles de connaissances (ce qu’elle sait déjà, ce qu’elle a pu apprendre grâce à l’innovation et grâce à l’imitation) :
13.3.3 Investissement et dynamique du capital
L’autre composante de la dynamique est donnée par l’investissement en capital productif des firmes et l’évolution de leur stock de capital physique.
où
- le dernier terme représente le stock de capital après dépréciation,
- les deux premiers termes de la fonction d’investissement représentent la marge moyenne et la part de marché de la firme,
- et le taux de profit représente la contrainte de financement de la firme (l’investissement possible ). Nelson et Winter considèrent aussi un financement possible par le secteur bancaire (il s’agit en fait plus d’une subvention publique à l’industrie).
Le désir d’investissement
résulte dans ce modèle du désir de la firme de modifier son stock de capital en vue d’ajuster son niveau de production à celle qu’elle aurait dans un équilibre de Cournot qui correspondraient à la distribution actuelle des productivités des firmes. Nelson & Winter suivent une idée centrale de [Schumpeter, 1935/1999] qui voit a dynamique économique sous la forme d’une succession de phases de perturbation résultant de l’introduction d’innovations majeures (machine à vapeur, chemins de fer, électricité, etc.) où la capacité de production de l’économie augmente après une phase de destruction de compétences (la fameuse destruction créatrice) et de phases d’allocation des biens ainsi créés (où le cadre d’équilibre walrasien lui semble un cadre d’analyse pertinent), jusqu’à l’arrivée des prochaines innovations majeures. [G] [G] Notons au passage que cette vision de l’évolution économique est très proche du concept d’équilibre ponctué développé à propos de l’évolution des espèces par [Gould, 1972]. Ainsi, ici, si le progrès technique s’arrête et les productivités des firmes ne changent plus, le comportement d’investissement des firmes les conduisent vers l’équilibre de Cournot correspondant. Tant qu’il n’y a pas de changement dans les productivités, l’industrie resterait alors à cet équilibre et seulement l’arrivée de la prochaine innovation qu’elle recommencera à bouger à nouveau. Par conséquent, tant que les innovations arrivent de manière fréquente, l’industrie ne converge jamais vers un équilibre de Cournot car l’équilibre change à chaque innovation et constitue par conséquent un cible mouvante qui n’est jamais atteinte.
Finalement, le taux d’investissement effectif est donné par :
toute possibilité de désinvestissement est exclue du modèle puisque l’investissement possible et l’investissement désiré contiennent tous les deux
Les deux équations dynamiques de transition du modèle sont donc :
Il s’agit d’équations récurrentes stochastiques non-stationnaires. Par conséquent, il n’est pas possible de résoudre le modèle analytiquement et on est obligé de procéder par simulations pour étudier le comportement de ce système.
13.3.4 Simulations informatiques
Pour étudier le comportement de ce système, on le formule sous la forme d’un ABM qu’on étudie grâce à des simulations informatiques pendant un nombre donné de périodes, après avoir fixé les valeurs de paramètres et les valeurs initiales des variables, comme nous l’avons discuté dans le chapitre 4↑.
Dans les analyses de Nelson & Winter,
et
sont initialisés de manières à garder le même niveau de dépense en R&D pour les différentes simulations et donc pour les différentes valeurs de autres paramètres. Le capital
aussi est initialisé selon cette règle et de manière à avoir un investissement désiré initial nul (donc correspondant aux niveaux de production d’équilibre de Cournot, étant données les productivités initiales des firmes).
Cela nous donne le tableau de valeurs Tab. 13.1↓.
| Nombre de firmes | ||
Tab. 13.1 Tab. des valeurs des paramètres dans les simulations de [Nelson, 1982]
Même ce modèle très simple fait alors apparaître des phénomènes très intéressants comme la concurrence entre les technologies, la dépendance au sentier et la co-évolution des parts de marché des firmes. Selon le régime retenu, des phénomènes de domination par une firme peuvent aussi apparaître (comme dans le régime cumulatif).
Prev Section 13.2: Développement des technologies
Up Chapitre 13: Dynamique des industries et des marchés
Section 13.4: Application : Nelson & Winter simplifié Next
Sommaire
(c) Murat Yildizoglu, 2021-
(c) Murat Yildizoglu, 2021-