Prev Section 11.4: Application : Oligopole de Cournot avec meilleures réponses et anticipations adaptatives simples
Up Chapitre 11: Evolution des anticipations et coordination
Section 11.7: Vision éco-systémique des anticipations : Irez-vous au Bar El Farol ce samedi soir? Next
11.5 Anticipations adaptatives élargies : Modèles mentaux et co-évolution des anticipations
Dans sa critique des modèles macroéconométriques de son temps, Robert Lucas, a souligné la difficulté d’évaluer des politiques alternatives, si on ne peut inclure dans cette évaluation la réaction optimale des agents à ces politiques [Lucas, 1976].
«Even to obtain the decision rules (...) then, we have to attribute to individuals some view of the behavior of the future values of variables of concern to them. This view, in conjunction with other factors, determines their optimum decision rules. To assume stability of [a macroeconometric relation] under alternative policy rules is thus to assume that agents’ views about the behavior of shocks to the system are invariant under changes in the true behavior of these shocks. Without this extreme assumption, the kinds of policy simulations called for by the theory of economic policy are meaningless.»[Lucas, 1976]
En effet, les modèles basés sur des anticipations adaptatives simples que nous avons introduites ci-dessus, sont sujets à cette Critique de Lucas, dans la mesure où les agents continuent, dans ce cas, à former leurs anticipations en supposant implicitement un processus dynamique invariant pour leurs erreurs. Or l’introduction de la politique économique risque de changer considérablement leur environnement économique (c’est même son objectif principal) et conduire à changer la dynamique de l’économie. Alors, sans une idée précise sur la manière dont les agents vont réagir à ces changements, on est démuni pour évaluer les effets des politiques économiques alternatives.
La solution que propose Lucas est l’intégration dans ces modèles des anticipations rationnelles proposées par [Muth, 1961]. Dans une formulation qui se veut quelque peu provocante, Muth présente sa théorie de la manière suivante :
"I should like to suggest that expectations, since they are informed predictions of future events, are essentially the same as the predictions of the relevant economic theory" (p. 316)
Ainsi, ces anticipations seraient conformes à ce que nous observerions sous les conditions d’optimalité des comportements et d’équilibre du marché. [A] [A] Muth précise un peu mieux sa formulation dans la suite de l’article :
"The hypothesis can be rephrased a little more precisely as follows: that expectations of firms (or, more generally, the subjective probability distribution of outcomes) tend to be distributed, for the same information set, about the prediction of the theory (or the "objective" probability distributions of outcomes).(ibidem)Par conséquent, même si ce concept peut séduire car elle augmente la cohérence de l’approche standard, en étendant le principe de la rationalité substantielle aux anticipations des agents, il ne nous est d’aucun secours pour analyser les dynamiques économiques hors équilibre.
Nous pouvons pourtant développer une approche alternative qui conserve la dimension purement inductive des anticipations basées sur les expériences passées des agents au sein de l’économie, tout en réduisant considérablement l’exposition à la critique de Lucas, car tenant compte du fait que la représentation du fonctionnement de l’économie que peuvent avoir les agents peut changer suite à la modification de leur environnement, à cause de l’introduction d’une politique économique ou de toute modification du comportement des autres agents qui les entourent.
En effet, nous pouvons considérer que les anticipations des agents sur les conséquences de leurs décisions et/ou sur l’état de l’économie résulte simplement des expériences qu’ils font avec le modèle mental [Holland, 1989] qu’il possède sur cette économie, ce modèle mental correspondant à la représentation qu’ils ont du fonctionnement de l’économie en fonction de leurs expériences passées et donc évoluant en fonctions de ces expériences pendant leur existence au sein de cette économie [101, 102]. Au moment de prendre une décision, l’agent considère alors les différentes alternatives qui s’offrent à lui à ce moment et fait des simulations (des expériences comme si) en utilisant son modèle mental pour évaluer les conséquences anticipées de ces alternatives comme le montre la figure 11.1↓. Il choisit alors une décision en fonction de ces anticipations et observe la conséquence effective de celle-ci. Si cette conséquence est différente de celle anticipée, l’agent utilise alors cette erreur pour corriger sa représentation de l’économie (son modèle mental) en tenant compte de cette nouvelle information. Par conséquent, quand son environnement change, l’agent est capable de tenir compte de ce changement dans ses anticipations et décisions futures. Il devient alors possible d’analyser les conséquences des politiques économiques alternatives en tenant compte que les agents vont adapter leurs comportements aux conséquences de ces politiques, sans qu’il soit pour autant nécessaire de supposer qu’ils devront tenir compte de l’équilibre de l’économie. Ces anticipations adaptatives ne sont pas soumises à la critique de Lucas, tout en étant compatibles avec une dynamique hors équilibre.
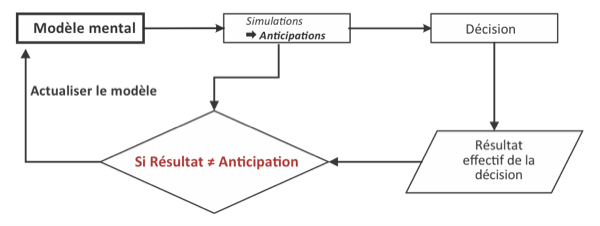
Figure 11.1 L’évolution du modèle mental [103]
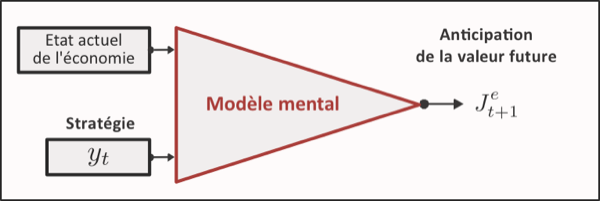
Comment pourrions-nous tenir compte d’un tel modèle mental et de son évolution? Le modèle mental doit permettre à l’agent d’établir des relations entre l’état actuel de l’économie, ses différentes décisions potentielles et les conséquences anticipées de ces décisions (Figure 11.2↓) et de faire des inférences grâce à ces relations.
Dans une première approche, nous pourrions imaginer, par exemple, que l’agent se comporte comme un économètre et estime une régression linéaire entre les conséquences de ses décisions passées et ses décisions, ainsi que les indicateurs sur l’état de l’économie contemporains avec ces décisions [Sargent, 1993]. Il est alors possibles d’imaginer que ce modèle évolue en fonction de nouvelles expériences, grâce à des estimations de moindres carrées récursives, comme l’ont envisagé Georges Evans et Seppo Honkapohja [Evans, 2001]. Cette approche imposerait alors une structure ad hoc (a priori linéaire) au modèle mental des agents et cela peut conditionner considérablement les dynamiques observées dans ce type de modèle. Il serait plus satisfaisant de ne pas contraindre ainsi la structure et l’évolution du modèle mental des agents.
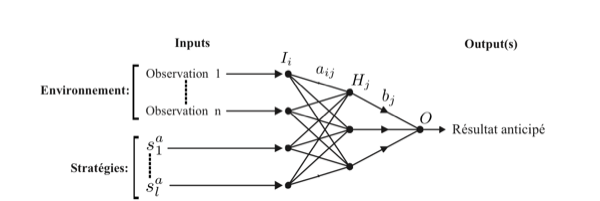
Une forme plus flexible, laissant plus de degrés de liberté à cette évolution nous semble possible grâce à l’utilisation des réseaux de neurones artificiels (RNA – [Anderson, 1990]). En effet, un RNA peut facilement représenter les relations que l’agent peut établir entre des inputs composés d’indicateurs pertinents pour son économie et les variables de décision avec la conséquence attendue de ces décisions (l’output du RNA) comme le montre la figure 11.3↓. Ces relations constituent le modèle mental de l’agent et nous pouvons même laisser la place pour des variables d’état implicites, qui n’ont de sens que pour l’agent, en incluant un niveau caché dans le RNA. On obtient alors une structure très flexible qui peut représenter des relations assez complexes entre les inputs et les outputs [Hornik, 1989]. Le nombre de noeuds au niveau caché est un paramètre qui module la complexité que nous supposons pour le modèle mental de l’agent. Comment cela fonctionne-t-il?
Les noeuds du RNA, sauf les inputs, agrègent les signaux qu’ils reçoivent et émettent des signaux vers le niveau suivant dans le RNA. L’agrégation se fait en général de manière non-linaire (grâce à une fonction de type sigmoïde par exemple) pour permettre l’apprentissage des relations non-linaires entre les variables. Un noeud du niveau caché va recevoir des signaux des
inputs
(correspondant ici aux observations et aux variables de décision) et va émettre un signal
vers le noeud d’output :
Le noeud d’output va alors agréger de la même manière tous les signaux provenant des noeuds du niveau caché et donner le résultat anticipé dans cet état de l’économie et avec ces valeurs des variables de décisions :
Les coefficients
correspondent au poids directs des différents inputs dans la détermination de l’output. Etant donnés les poids
, le RNA est capable d’attribuer un résultat attendu à toute combinaison des valeurs des inputs, même si l’agent est confronté pour la première fois à cette combinaison : c’est cette capacité de généralisation du RNA qui permet à l’agent de former des anticipations pour des situations qu’il rencontre pour la première fois, et des stratégies qu’il teste pour la première fois.
Ces poids évoluent en fonction des erreurs observées dans le passé entre les résultats anticipés et les résultats effectifs observés à la suite de l’implémentation de la décision choisie par l’agent à chaque période. Suite à une telle erreur, les poids
et
sont augmentés ou réduits, étant donnée la dérivée, par rapport à chaque noeud, de la fonction d’activation
, en commençant par le noeud d’output en propageant des corrections vers les noeuds d’input [Masters, 1993]. Par conséquent, un tel RNA, ajusté avec un flux continu de données résultant des expériences de l’agent dans son environnement constitue un modèle variant dans le temps en fonction de ces expériences de l’agent et peut être utilisé pour représenter le modèle mental de l’agent et son évolution, avec relativement peu d’hypothèses sur la structure du modèle (principalement, le nombre de noeuds au niveau caché).
On peut alors combiner un tel modèle mental avec une méthode d’exploration de l’espace des stratégies (un algorithme génétique ou simple expérimentation aléatoire) et une méthode de sélection de stratégies, guidée par les anticipations formées sur leur conséquence grâce à ce modèle mental, pour représenter un comportement à rationalité procédurale des agents, parfaitement opérationnel hors équilibre, et robuste par rapport à la critique de Lucas.
Cette approche s’est révélée très fructueuse sur des questions économiques assez différentes. [109] montre que les firmes suivant une telle procédure pour déterminer leur stratégies d’investissement en R&D dans le modèle de dynamique industrielle de Nelson & Winter (voir la partie suivante) peuvent exhiber un comportement assez réaliste. [110] montre que des consommateurs suivant une telle procédure peuvent apprendre la règle de consommation buffer-stock de [Carroll, 1992]. [112] montre qu’une banque centrale avec de telles anticipations adaptatives peut guider l’économie vers l’optimum social dans le modèle de [Kydland, 1977], contrairement au résultat négatif obtenu par ces auteurs avec des anticipations rationnelles. Tous ces travaux ont aussi l’avantage de nous permettre d’analyser la co-évolution endogène des modèles mentaux et des anticipations des agents.
[Arthur, 1994] adopte une approche plus directement éco-systémique pour étudier cette co-évolution, comme nous allons le voir après l’application suivante.
Prev Section 11.4: Application : Oligopole de Cournot avec meilleures réponses et anticipations adaptatives simples
Up Chapitre 11: Evolution des anticipations et coordination
Section 11.7: Vision éco-systémique des anticipations : Irez-vous au Bar El Farol ce samedi soir? Next
Sommaire
(c) Murat Yildizoglu, 2021-
(c) Murat Yildizoglu, 2021-