Prev Section 10.7: Dynamique et émergence de l’ordre
Up Chapitre 10: Motivations individuelles et coordination collective
Section 10.9: Application : Apprentissage individuel dans l’Oligopole de Cournot Next
10.8  Application : Emergence de la ségrégation urbaine [Schelling, 1971]
Application : Emergence de la ségrégation urbaine [Schelling, 1971]
Il s’agit d’un modèle très simple, qu’on peut même étudier à l’aide d’un damier, de plusieurs pièces de deux types et des dés. La version NetLogo vous permettrait de faire plus facilement des expériences avec ce modèle.
10.8.1 Description des éléments du modèle :
- Les individus choisissent leur localisation dans l’espace (une ville) représenté comme un damier de cases, pour simplifier
- Une population de taille , formée de deux types d’individus (représentés par leur couleur rouge ou vert)
- Le type de chaque individu est déterminé dès le début, selon un tirage aléatoire (pile ou face)
- Chacun accepte a priori d’avoir des voisins de l’autre type avec un seuil de tolérance
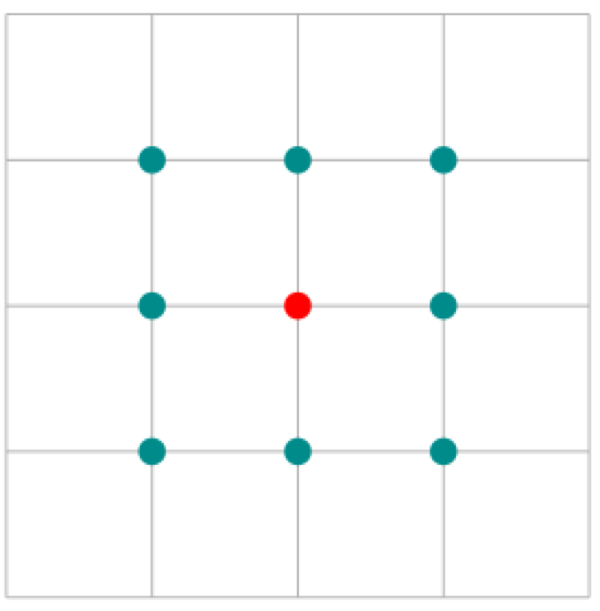
- A chaque moment, chaque individu (indiqué en rouge) observe ses voisins immédiats (indiqués en vert) sur le damier (voir Figure 10.3↑).
-
Si la proportion des voisins de l’autre type est supérieure à
, l’individu décide de déménager :
- Il bouge vers une case choisie aléatoirement,
- si la case choisie est occupée, il retire une nouvelle case aléatoire, jusqu’à ce qu’il trouve une case vide.
10.8.2 Programme NetLogo
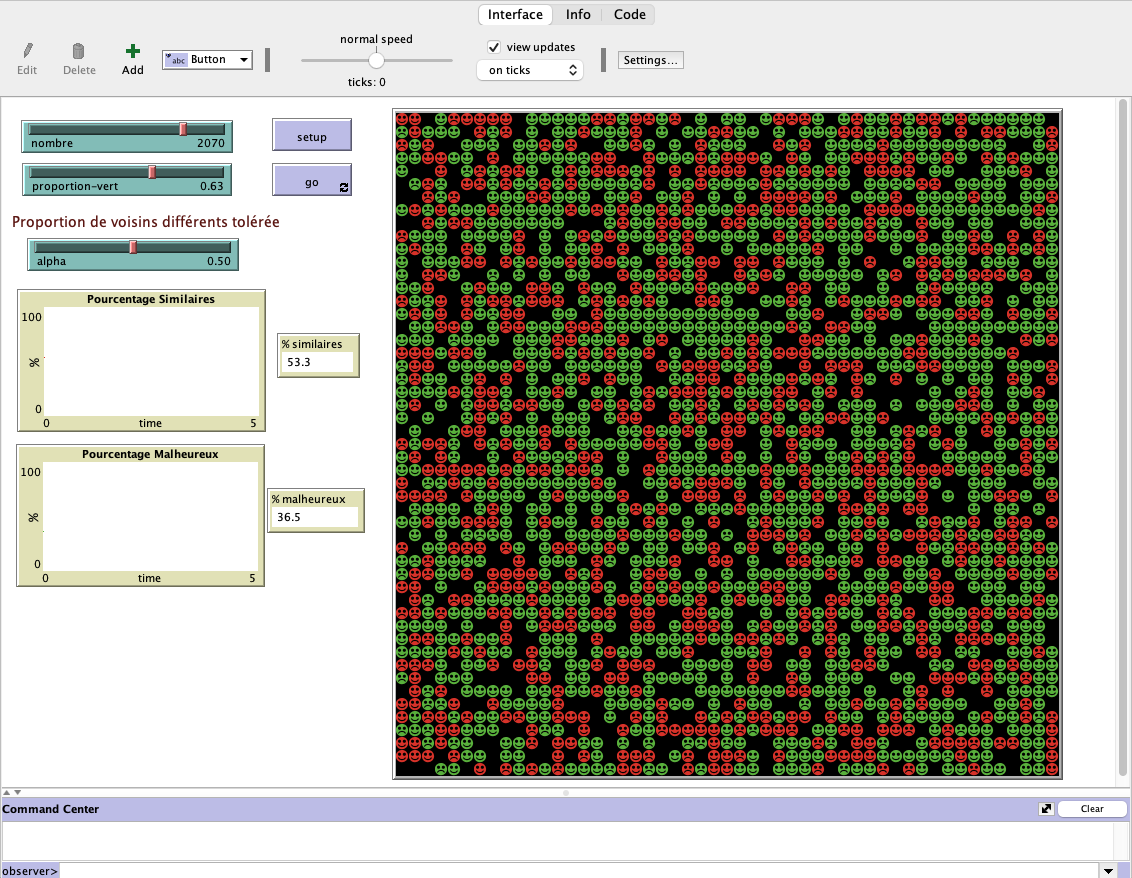
L’interface visuelle doit contenir (voir par exemple Figure 10.4↓) :
- Un Monde (World) représentant l’espace urbain, avec une taille cases (Origine=Center; ; ; Wraps horizontally et vertically; Patch size = ).
- Un curseur (slider) permettant de sélectionner des valeurs allant de à , par pas de , pour le nombre d’individus (appelez la variable correspondante nombre).
- Un curseur permettent de sélectionner des valeurs allant de à ; par pas de , pour le seuil de tolérance (appelez la variable correspondante alpha).
- Un indicateur (observer) qui donne le pourcentage d’individus heureux dans la population : tauxHeureux (+ graphique – optionnel).
- Un indicateur (observer) qui donne le pourcentage moyen de voisins similaires autour des individus : tauxSimilaire (+ graphique – optionnel).
- Un bouton «Setup» permettant l’exécution de la procédure setup (voir ci-dessous).
- Un bouton «Go» permettant l’exécution continue de la procédure go jusqu’à ce que tous les individus sont heureux.
Le code doit contenir :
-
Déclaration des variables globales et des variables pour les individus :
- Les variables globales déclarées au début du code : taux-similaire et taux-malheureux qu’on va observer dans les résultats.
- Les espèces (breed) de tortues que nous allons avoir dans le modèle : nous allons avoir un seul type que nous allons appeler individu au singulier et individus au pluriel.
- Les variables spécifiques à chaque individu : heureux?; voisins-similaires; voisins-differents; voisins-tous.
- Le type de l’individu sera déterminé par sa couleur, mais nous n’avons pas besoin de déclarer une variable couleur car chaque tortue possède par défaut une variable color.
-
Une procédure setup qui initialise le modèle, qui crée les individus, les affecte aléatoirement aux deux types et les place aléatoirement sur le damier :
- Initialisation de l’environnement de simulation: clear-all;
- Création de nos individus en utilisant la variable globale nombre;
- Parmi ces nombre individus, une moitié auront la couleur rouge et l’autre la couleur verte, les individus de chaque moitié étant choisis aléatoirement (Astuce : pour choisir aléatoirement la couleur et la localisation des individus, demander aux patchs de créer les individus sur eux – sprout);
- On va calculer les indicateurs individuels et collectifs de bonheur une première fois;
- Préparer les périodes en exécutant reset-ticks.
-
Une procédure go qui contient les instructions correspondant au déroulement d’une période dans le modèle :
- Calcul, au début de la période, de l’état de chaque individu (heureux ou malheureux) en fonction du seuil de tolérance et les types de ses voisins.
- Condition d’arrêt (stop) de la simulation : si tous les individus sont heureux;
- Déplacement des individus malheureux jusqu’à ce qu’ils trouvent une case libre sur le damier : l’individu malheureux choisit une direction aléatoire entre et et il fait un nombre de pas aléatoire entre et ; si la case qu’il découvre est déjà occupée, il recommence.
- Calcul des indicateurs indiqués ci-dessus et actualisation des graphiques le cas échéant.
- On augmente le compteur de période d’une unité (tick)
- Vous pouvez choisir d’effectuer certaines opérations dans des sous-procédures si cela vous parait intéressant, comme le calcul des indicateurs individuels et collectifs par exemple.
10.8.3 Expériences
Ce modèles est extrêmement simple. Les seules dimensions sur lesquelles nous pouvons mener des expériences sont la taille de la population
(donc la taille de l’espace vide sur le damier, par complémentarité) et le seuil de tolérance
des individus.
-
Fixer
- Fixer et exécuter le modèle. Observez le temps que le modèle met à trouver une configuration stable (arrêtez en cliquant sur le bouton Go s’il met trop de temps). Quel est le pourcentage moyen de voisins similaires ? Mettez cette observation en rapport avec la valeur de .
- Même question pour .
- Faites varier entre ces deux valeurs extrêmes pour étudier la relation entre la tolérance des individus et la taux de ségrégation qui en résulte. Notamment, étudiez les valeurs suivantes pour : . Est-ce que vous observez un effet de seuil?
- Fixer . Même question que ci-dessus, mais en faisant varier cette fois-ci. Considérer les valeurs suivantes pour : .
- Discutez ces résultats quant à la relation qui existe entre les motivations individuelles et le résultat collectif qui en résulte.
Instructions NetLogo à découvrir dans le dictionnaire : clear-all, ask, n-of, patches, count, sum, all?, any?, other, ask turtles with, random-float, rt, fd, move-to, patches-here, turtles-here, turtles-on, neighbors, myself, stop.
Prev Section 10.7: Dynamique et émergence de l’ordre
Up Chapitre 10: Motivations individuelles et coordination collective
Section 10.9: Application : Apprentissage individuel dans l’Oligopole de Cournot Next
Sommaire
(c) Murat Yildizoglu, 2021-
(c) Murat Yildizoglu, 2021-