Prev Chapitre 7: Évolution in silico
Up Chapitre 7: Évolution in silico
Section 7.2: Application : Le jeu de la vie de Conway Next
7.1 Le jeu de la vie de Conway : un jeu avec des règles simple
John Conway va s’inspirer de l’un des travaux de von Neumann pour inventer un jeu très simple qui permet de tester cette capacité des formes très simples à développer et préserver «la vie» pour, dans un univers très dénudé et avec des règles élémentaires.
Il s’agit d’un jeu très simple qui se joue sur un damier. Les cases du damier possèdent deux états possibles : l’état mort et l’état vivant. Chaque case possède huit voisins immédiats (voir Figure 7.1↑).
L’état de chaque case évolue d’une période à l’autre selon trois principes élémentaires :
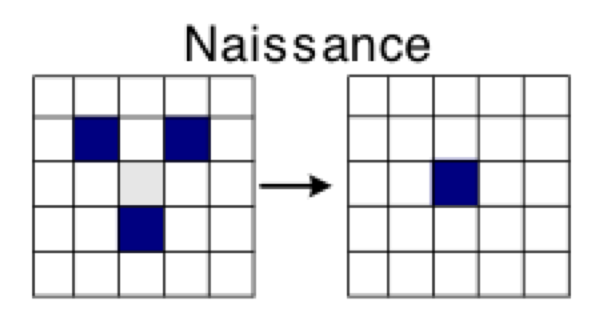
Principe de naissance : Si la case est morte mais exactement trois de ses voisins sont vivants, alors elle devient vivante (voir ci-dessous Figure 7.2↓-a).
Principe de conservation : Si elle est vivante elle reste vivante si elle a deux ou trois voisins actifs.
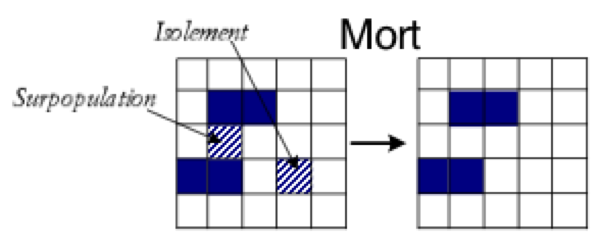
Principe de sous-population : Si elle est vivante mais elle a moins de deux voisins vivants, alors elle meurt (voir Figure 7.2↓-b)
Principe de surpopulation : Si elle est vivante mais elle a plus de trois voisins vivants, elle meurt (voir Figure 7.2↓-b).
Les règles du jeu sont donc très simples. Ainsi, pour connaitre l’état suivant d’une case (quelque soit son état actuel) il suffit de compter ses voisins immédiats (cases occupées) :
- s’il y en a exactement deux la case conserve son état;
- s’il y en a exactement trois, la case reste ou devient vivante;
- sinon la case meurt.
Quand on applique ces règles très simples de manière répétée, de période en période, à partir d’une configuration initiale donnée du damier, avec certaines cases vivantes, nous observons une gamme très diversifiée et riche de dynamiques sur le damier : reproduction à l’identique de la configuration, évolutions cycliques, disparitions, transformations et développement, etc. Ces règles constituent ainsi des mécanismes de sélection et de génération de diversité et cela est à la base de la richesse du jeu de la vie qui a fasciné autant de chercheurs depuis l’invention de Conway. Cette fascination a aussi permis l’émergence de tout un domaine de recherche sur les dynamiques de systèmes d’un type particulier : les automates cellulaires dont fait partie le Jeu de la vie de Conway [Wolfram, 2002].
Liens :
- Logiciel et applet pour simuler le jeu de la vie de Conway : Golly
Prev Chapitre 7: Évolution in silico
Up Chapitre 7: Évolution in silico
Section 7.2: Application : Le jeu de la vie de Conway Next
Sommaire
(c) Murat Yildizoglu, 2021-
(c) Murat Yildizoglu, 2021-