In the beginning of each period, each firm is characterized by its productivity and its capital stock.
Two main blocs:
![]() productivity of capital (
productivity of capital ( ![]() : coefficient of capital) of
firm
: coefficient of capital) of
firm ![]() at date
at date ![]() ,
,
![]() : capital stock of firm
: capital stock of firm ![]() at date
at date ![]() .
.
Capital is the only input. The unit using cost of capital is ![]() .
.
Constant returns to scale.
Productivities are modified by technical progress.
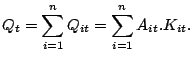
(![]() firms in the market)
firms in the market)
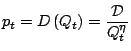
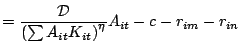 |
The productivities are modified in each period consequently to the technical progress.
Innovation is a two-stage stochastic phenomenon
![$\displaystyle P\left[ d_{int}=1\right] =a_{n}\underset{\text{Innovative R\&D}}
{\underbrace{r_{in}K_{it}}},
$](img15.gif)
There is three possibilities concerning the result of innovation
| with |
For the imitation, we have one stochastic draw which determines if the firm's R&D investment has been successful.
If it is the case, the firm obtains the best practice in the industry
![]() :
:
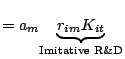 |
||
Finally, the effective productivity of the firm for the next period is given by the best of these three outcomes:
Investment in physical capital is the other source of dynamics in the model.
In the general case, the new capital stock of the firm will be given by:
where the last term takes into account the depreciation of capital.
More specifically, in the model of Nelson and Winter, firms adjust their capital stock in accordance with their Cournot conjectures.
Desired investment results from the comparison of the actual margin of the firm with its target margin reflecting its market power.
The relative mark-up rule of Cournot duopoly can also be formulated as a
comparison between the market price ![]() and the expected price of the firm,
and the expected price of the firm,
![]() :
:
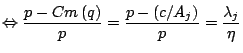 |
||
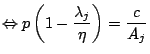 |
||
This expected price is increasing with the market share of the firm
![]() and its capital cost, and it is decreasing with the
elasticity of demand
and its capital cost, and it is decreasing with the
elasticity of demand
![]() and the productivity of the firm.
and the productivity of the firm.
If this price is lower than the market price, the marginal profit is positive and the firm considers that it must increase its output.
The only way of increasing the output is investment: The investment should over-compensate the depreciation of capital:
where ![]() is the desired rate of investment and
is the desired rate of investment and ![]() , the depreciation rate.
, the depreciation rate.
The firm can finance this investment by the profit and, if the profit is positive, also by borrowing from the financial system.
This gives the possible investment rate:
The capital stock of the firm is therefore given by:
These Cournot-conjectures correspond to a strong rationality for the firm.
Each firm knows the elasticity of market demand, its market share, and can compute the optimum that is implicitly given in the expected price.
To this price correspond an optimal output level and stock of capital. ![]() is only one possible way of adjusting the effective capital to this optimal capital.
is only one possible way of adjusting the effective capital to this optimal capital.
This equation, combined with the equation
![]() gives
the transition law of the system:
gives
the transition law of the system:
We have a non-stationary Markov system which entails simulation studies.