$\newcommand{\lyxlock}{}$

Warning: MathJax requires JavaScript to correctly process the mathematics on this page. Please enable JavaScript on your browser.

Prev Section: What about sequential games? Up Main page Section: What about incomplete information? Next

Subgame Perfect Nash Equilibrium (SPNE)

Until this point, we have considered

The importance of strategic interactions
How we can read any interactive context as a game by clarifying
Different components of a game (players, strategies, outcomes, payoffs)
How we can represent such a game
Different dimensions that structure this representation (nature of interactions, their sequentiality, information of players)
A first and limited solution concept: elimination of dominated strategies
Nash equilibrium
Sequential games and information sets
Possibility of a better solution concept for sequential games: SPNE

Subgame perfect Nash equilibrium (SPNE) is based on the following ideas.

Each player now considers that her choices would only be followed by decisions that are optimal for each following player, when it is this that player’s turn to play.

To test a Nash equilibrium for subgame perfectness, we need to check if each of the actions corresponding to this Nash equilibrium will actually be used by the corresponding players during the actual game sequence.

How to check ? For each Nash equilibrium, follow the game tree and ask at each step, locally, if the corresponding player would actually choose the action supporting this NE.

To do this this, we need to analyze all decisions locally, independently from what is happening in the rest of the game. Hence the idea of determining the subgames of the game tree where such an analysis may be correctly done :

A subgame is a section/subset of the game tree in which we can analyze the decisions of the involved players separately from the rest of the game

Such an analysis is only possible iff this subset itself is a complete game:
A subgame starts with an initial decision node (as any sequential game)
If a node is part of this subgame, all nodes that follow it must be included
until the terminal nodes following these nodes (and the corresponding payoffs), otherwise we cannot compare payoff to check the optimality of actions
if a node included to the subgame belongs to an information set containing another node, the latter also must be included in the subgame (since the decisions in these two nodes cannot be made/analyzed separately)

Each game possesses at least one subgame: the game tree itself. Each subgame different from the game itself is called a proper subgame.

We can now precisely define the Subgame Perfect Nash Equilibrium concept proposed by Reinhard Selten.

[Selten, 1975]: A Nash equilibrium of the full game is also a SPNE if the choices that support it are all part of the Nash equilibria of each subgame.

Checking the strategies of the players as supports of a SPNE means that we assume that each player is smart/rational enough to anticipate the rest of the game that can currently result from her/his choices at each step: She must check if the choices by the following players are optimal in each corresponding subgame.

So, we must check, subgame by subgame, the optimality of each decision supporting the NE.

This can quickly become quite cumbersome in any fairly complex game.

There must be a better way

To search for SPNE, we can adopt a backward induction approach:

We start by determining the NE of the subgames closest to the end of the game (to its terminal nodes and payoffs)
We reduce the game tree by replacing each of these subgames by one of their NE
We consider the next subgames containing the ones we have replaced by their NE, and determine their NE
We continue until we have the subgame starting at the initial node of the game
This node is now followed only by decisions that will really be chosen by the players in the rest of the game, by construction
and its NE, if its exists, is necessarily a SPNE!

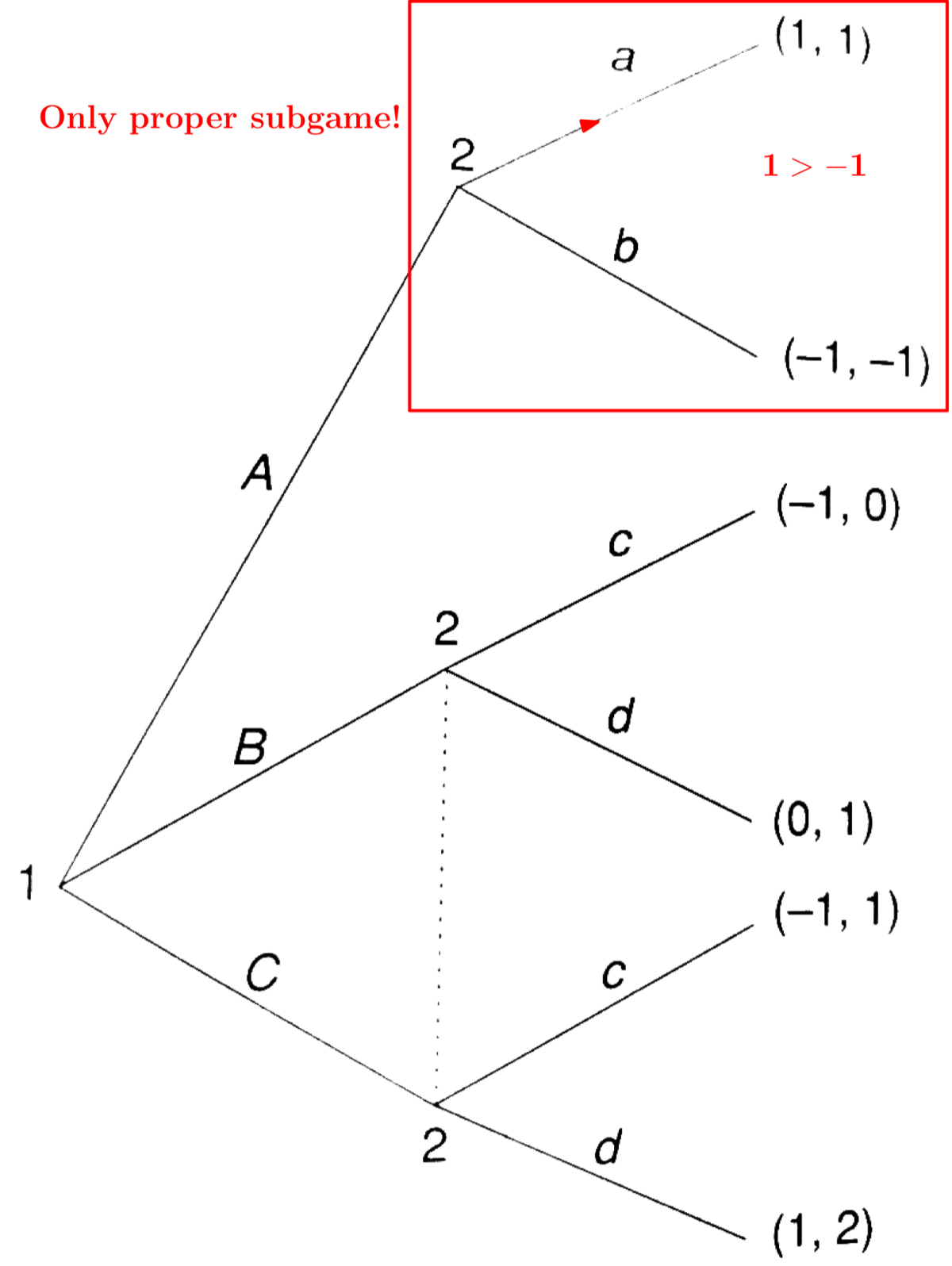
figure images/example-vega-redondo-3b-2.png

Example: An example (Vega-Redondo 2003) : Subgames?

Animated version

A more complete example: The game of entry

An new firms considers the possibility of entering in the market of an incumbent monopoly. In order to enter, its preferably should install some production capacity to be able to produce with low marginal costs if ever she enters. Observing the behavior of this firm, the incumbent can choose to increase his production capacity in order to invade the market. The potential entrant cannot observe the choice of the incumbent when it must decide to produce and offer her product in the market. The sequence of decisions is represented in the following game tree and the payoffs of the firms result from different situations in terms of market sharing and costs.

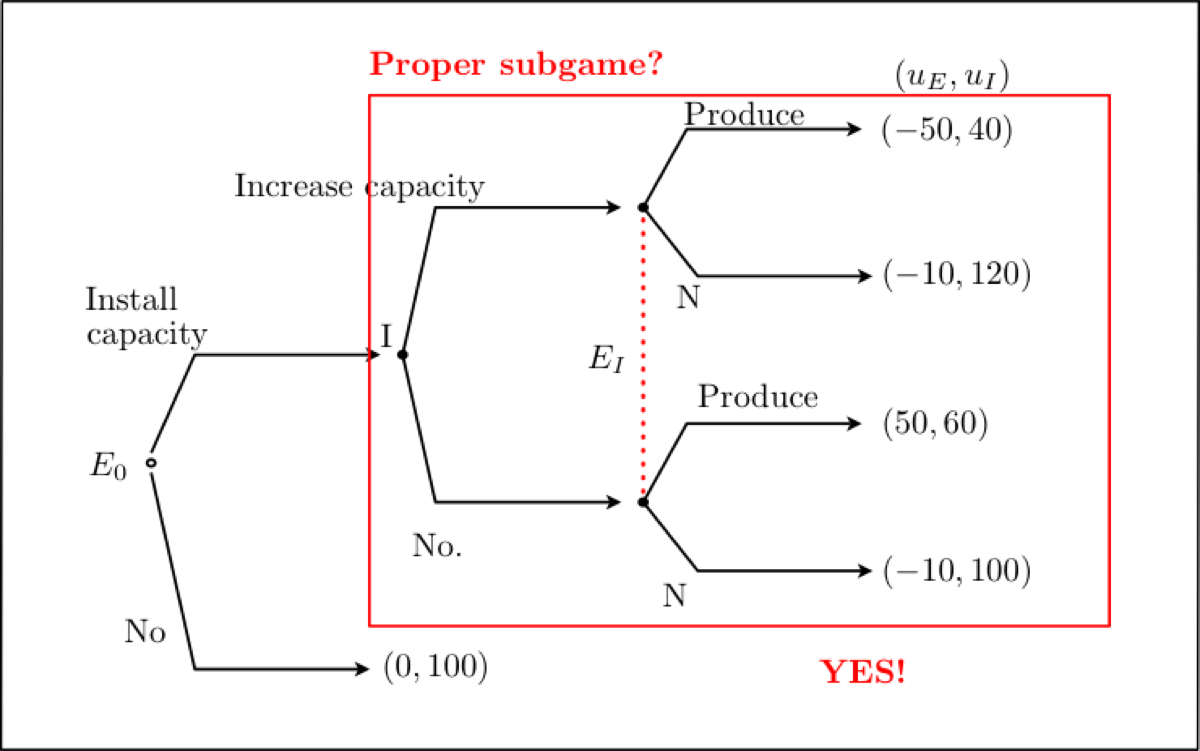
The entry game: I : Incumbent firm ; E: Potential entrant

Animated version

The game has only one proper subgame and we need to check the Nash equilibrium of this subgame.

If we find any, we can reduce the game tree by replacing this subgame by its equilibrium.

Indeed the firm E, when it considers the relative value of its two potential decisions, at the node

, will anticipate that the choice “Install capacity” would be followed by the NE of the subsequent subgame:

figure images/entree2-epsj-2-En-reducedgame-0.png

In this subgame we have two players: I and E:

I must choose to increase capacity or not
and E must choose to effectively enter the market by producing or not

The outcomes and the corresponding payoffs result from these choices.

We can represent this subgame in normal form to easily determine its NE.

We will put E in line, so we can keep the same order of the payoffs in the game matrix:

	I
		.
E

We can easily determine the best replies of these player in this subgame:

	I
		.
E

Two intersections between best replies, hence we have two NE in this subgame:

E stays out of the market, entry is blocked by I: I’s threat of increasing capacity is credible!
E enters the market, and we have a duopoly.

, E will now anticipate that “Install capacity” could be followed by

. Depending of her expectations, we could have two reduced games:


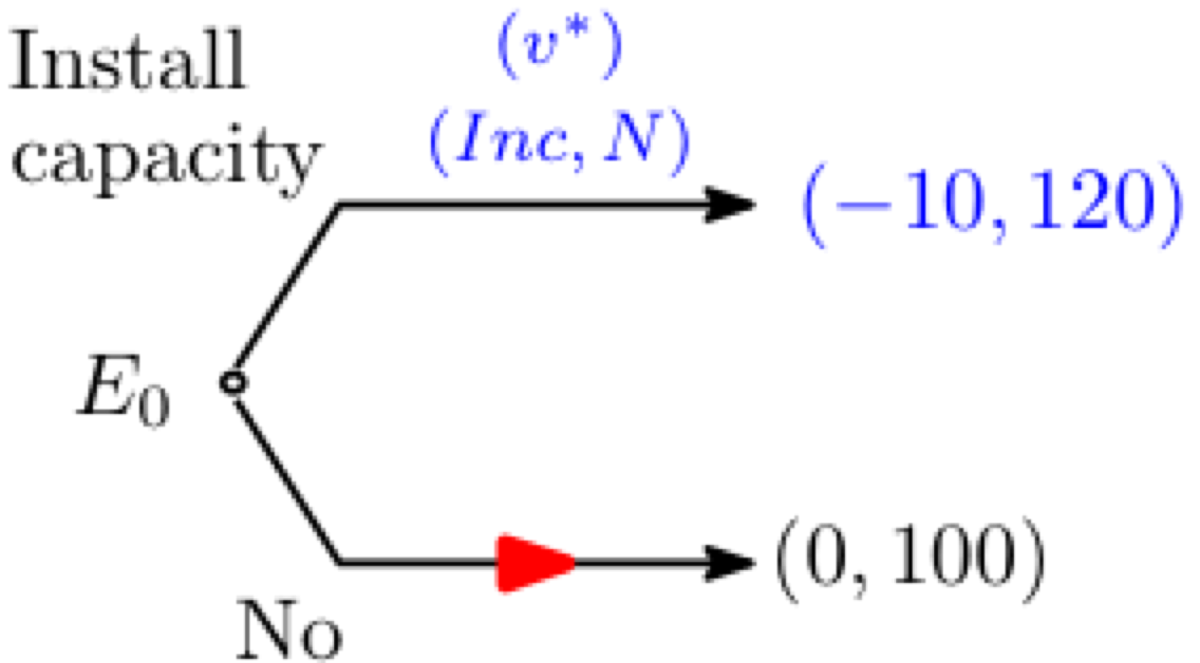
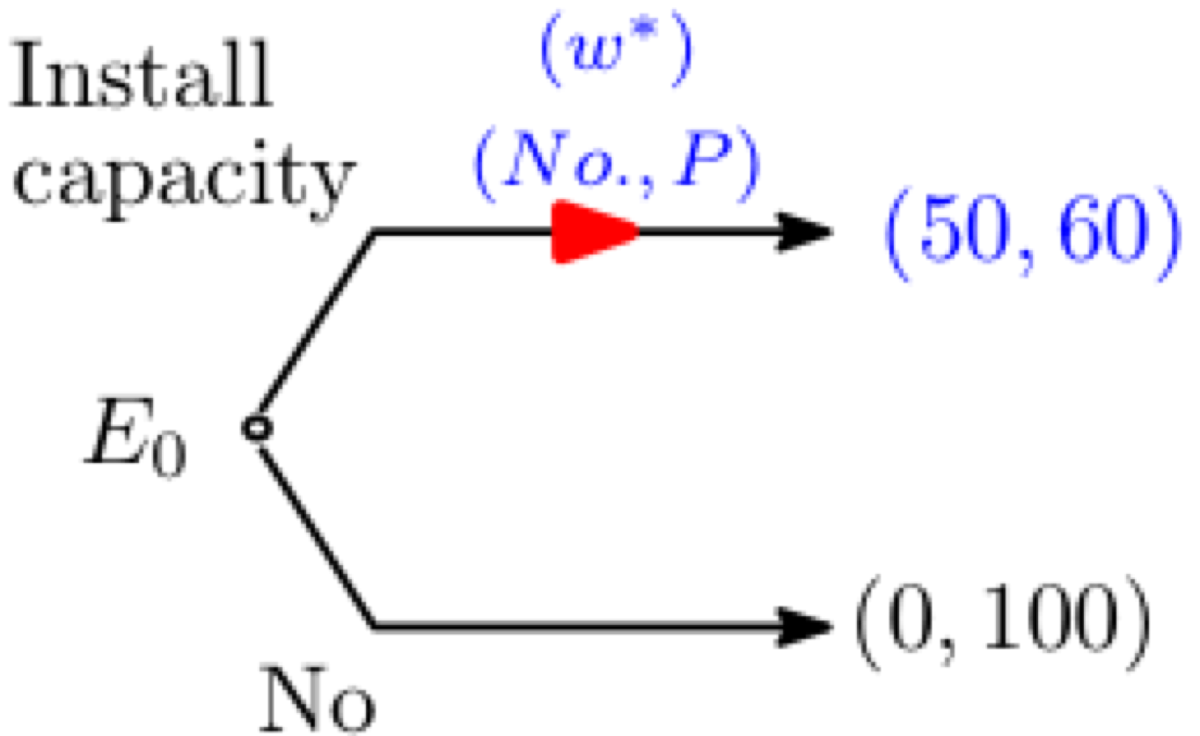
(a)	(b)

Consequently, we have two SPNE in this game:

(a) E anticipates that her choice will be followed by and prefers to not Install any capacity.
(b) E anticipates that her choice will be followed by and prefers to install capacity and enter and produce on the market. We have a duopoly in this case.

We can represent the equilibrium paths in these two cases:

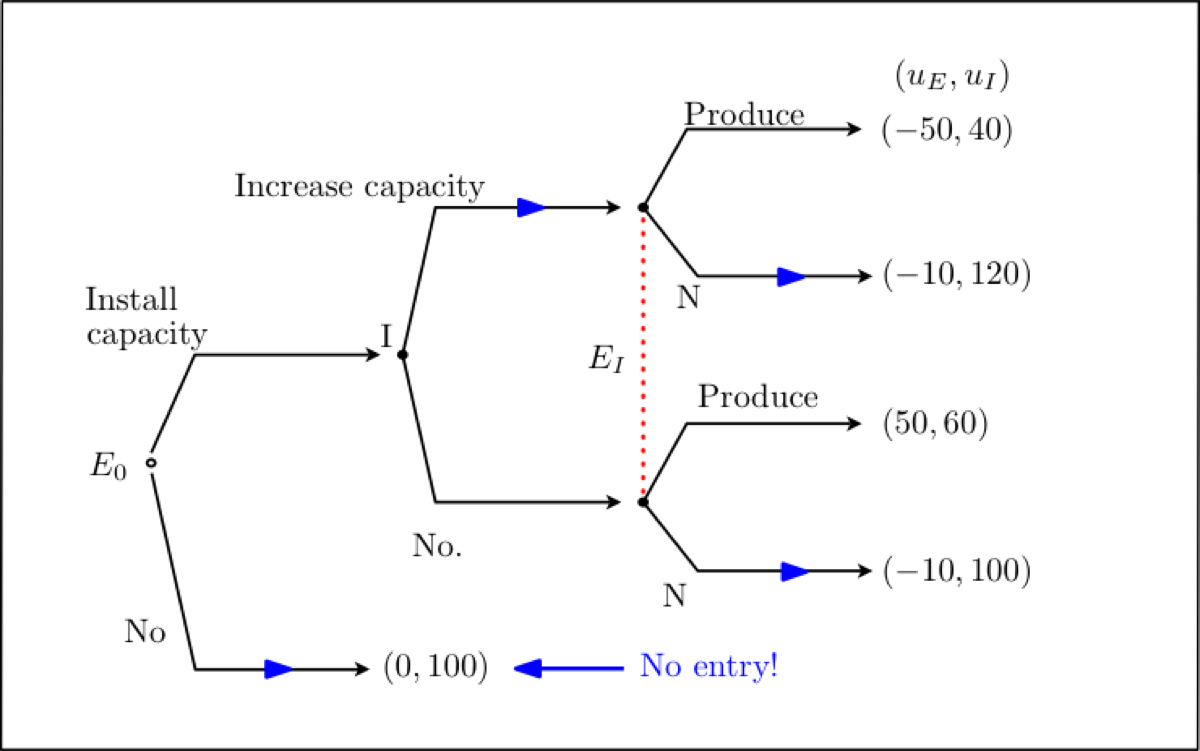
figure images/entree2-epsj-2-En-SPNE-tree-0.png

Equilibrium (a)

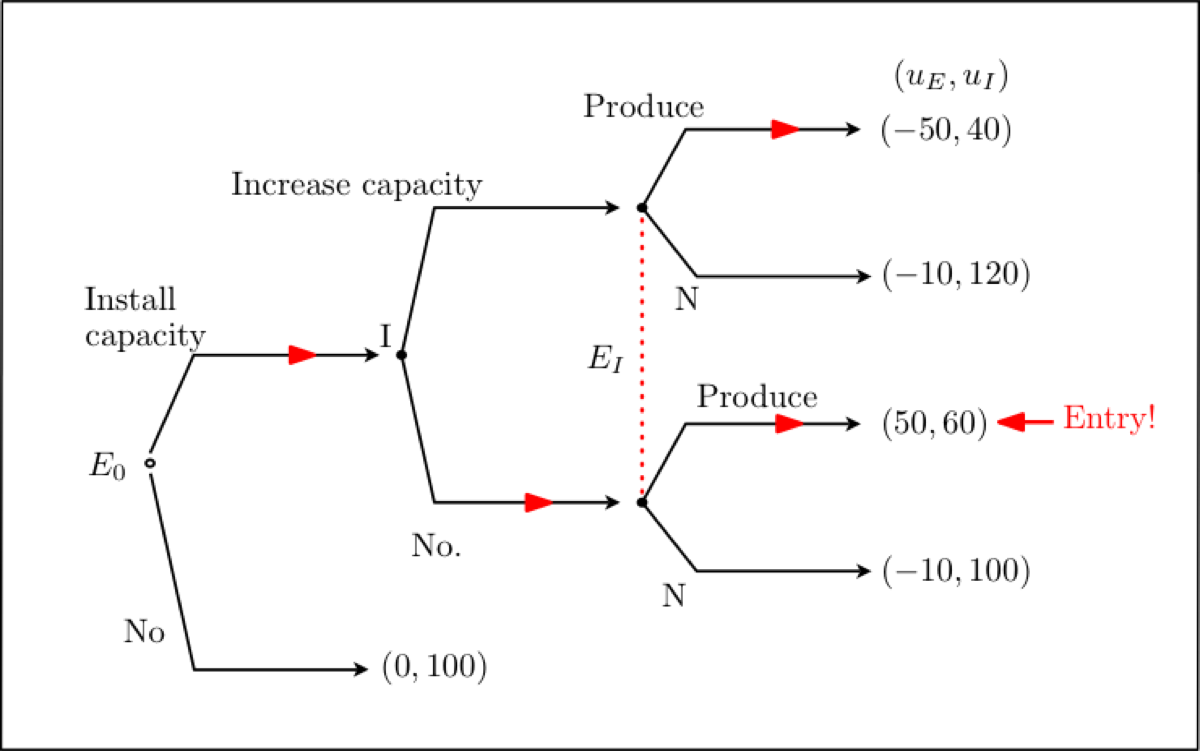
figure images/entree2-epsj-2-En-SPNE-tree-1.png

Equilibrium (b)

There is a third NE in this game but we have not seen it because it does not resist to the test of subgame perfection.

In this NE, I increases capacity, E does not install capacity but produces nevertheless. But the outcome

does not belong the set of NE of the subgame (otherwise, we would have seen it).

We observe that subgame perfection may reduce the set of equilibria but this solution concept also is prone to the multiplicity problem, even if it requires stronger rationality from the agents (they must anticipate only the NE of the subsequent subgames will follow their choices).

Nevertheless, the SPNE is rather a more natural solution concept in sequential games than the NE.

Prev Section: What about sequential games? Up Main page Section: What about incomplete information? Next

Sommaire
(c) Murat Yildizoglu, 2021-